들어가기에 앞서...
회귀분석 수업을 듣고 선형대수 관점에서 PCA(주성분 분석)를 정리한 글입니다. 제가 공부하고 이해한 선에서 글을 적다 보니, 잘못된 내용이나 표현이 있을 수 있습니다. 그런 부분에 대한 지적은 댓글로 남겨주시면 감사하겠습니다. :)
PCA(주성분 분석)와 다중공선성
다중회귀분석을 하기 위해서는 만족해야 하는 가정이 몇 가지 있습니다. 그중 한 가지가 바로 '독립변수들 간의 다중공선성이 없어야 한다'는 것입니다. 회귀분석에서 다중공선성이란 독립변수들 간에 강한 상관관계가 나타나는 문제를 뜻합니다. (이를 수학적으로는 어떤 독립변수가 다른 독립변수들과 선형 독립이 아닌 경우라고 표현할 수 있습니다.)
이러한 문제를 해결하기 위한 방법 중 하나가 바로 PCA입니다. PCA는 고차원 공간의 표본들을 선형 연관성이 없는, 즉 선형 독립인 저차원의 공간으로 변환하는 방법으로, 원 데이터의 분산을 최대한 보존하는 새로운 기저(=축)를 찾는 것이 그 목적입니다.

간단한 데이터셋을 좌표 위에 나타내서 이해해보도록 하겠습니다. 이 데이터셋을 평범한 (x, y) 좌표에 나타낸 결과는 왼쪽과 같습니다. x가 커짐에 따라서 y가 커지는 경향, 즉 x와 y의 선형 상관관계를 확인할 수 있습니다. 이런 x, y를 그대로 회귀분석의 독립변수로 이용할 경우에는 회귀 계수의 p-value 값이 크게 나타나며 회귀 계수가 유의하지 않은 문제가 발생할 수 있습니다.
이런 경우에는 새로운 기저(축), 즉 주성분을 기준으로 데이터를 바라보는 것이 도움이 됩니다. 뒤에서 차차 보이겠지만 주성분은 데이터의 분산이 가장 큰 방향을 가리키는 벡터를 의미합니다. 위의 데이터셋에서는 빨간 벡터, 녹색 벡터가 주성분이 됩니다. 두 벡터가 x축, y축과 같은 방향을 가리키게 그래프를 회전시킨 결과가 바로 오른쪽 그래프입니다. 왼쪽 그래프와 달리 변수 간 상관관계라 사라진 것을 확인할 수 있습니다. 이것이 바로 PCA를 사용하는 이유입니다.
PCA를 위한 선형대수
PCA를 수학적으로 해석하기 위해서는 몇 가지 선형대수 지식이 필요합니다. PCA를 잘 이해하기 위해서는 이러한 선형대수 내용을 수리적으로 또 기하학적으로 이해하는 것이 도움이 됩니다. 부족하지만 이해한 대로 내용을 정리해보았습니다.
선형 변환(Linear transformation)
어떤 벡터 x에 행렬 A를 곱한 결과를 벡터 b라고 할 때, 그 식은 $Ax=b$으로 나타낼 수 있습니다. 행렬 A를 이용해 벡터 x를 벡터 b로 변환하는 이러한 함수를 선형 변환이라고 합니다.
고윳값과 고유 벡터(Eigen vector & Eigen value)
$Ax=b$와 같이 어떤 벡터에 행렬 A를 곱해주면 새로운 벡터로 매핑이 되게 됩니다. 그런데 몇몇 벡터는 선형 변환 전/후에도 방향 변화가 일어나지 않습니다.
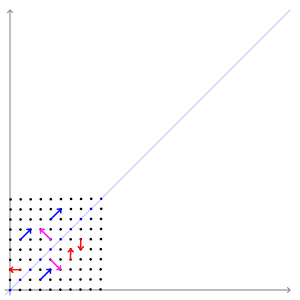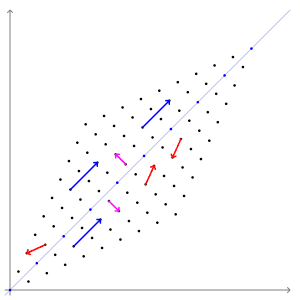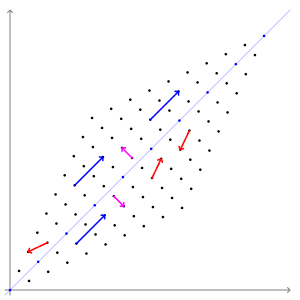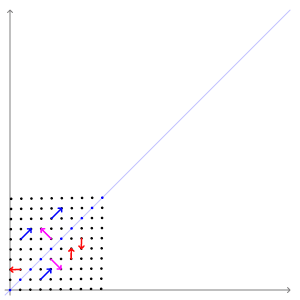
위의 애니메이션에서는 빨간색 벡터와 달리 파란색 , 분홍색 벡터들은 선형 변환 전/후에 방향 변화가 없는 것을 알 수 있습니다. 길이는 늘어나지만 그 방향은 전혀 변하지 않습니다. 이 두 벡터의 방향이 변하지 않는 이유는 두 벡터가 곱해지는 행렬이 향하는 방향(=벡터를 투영하는 방향)을 나타내기 때문입니다. 두 벡터가 입력 벡터의 크기를 늘이거나 줄이는 기준이 되는 축이 된다고도 생각할 수 있습니다. 이러한 벡터를 우리는 '고유 벡터'라고 부릅니다.
행렬 A의 고유 벡터는 행렬 A를 곱하더라도 방향이 변하지 않고 그 크기만 변합니다. 이를 수식으로 나타내면 다음과 같습니다. 이 방정식에서 A는 행렬, x는 벡터, λ는 스칼라 값입니다. 아래의 식을 만족하는 x가 고유 벡터, λ가 고윳값이 됩니다.

공분산 행렬(Covariance Matrix)
공분산 행렬은 서로 다른 변수의 모든 조합에 대한 공분산을 한꺼번에 표기하는 행렬로, 두 변수가 어떤 상관관계를 가지는지를 알 수 있는 행렬입니다. PCA를 통해 데이터의 분산이 가장 큰 방향을 향하는 벡터를 뽑아내야 하기 때문에 그 과정에서 공분산 행렬이 등장합니다.
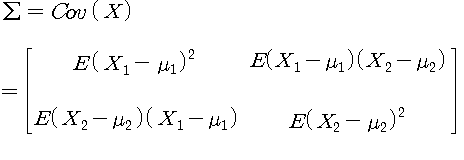
PCA(주성분 분석)
위에서 언급한 선형대수 개념을 가지고 PCA를 이론적으로 유도해보도록 하겠습니다.

위와 같은 다중회귀분석을 한다고 생각해보겠습니다. 변수 개수는 p개, 관측치는 n개인 상황입니다.
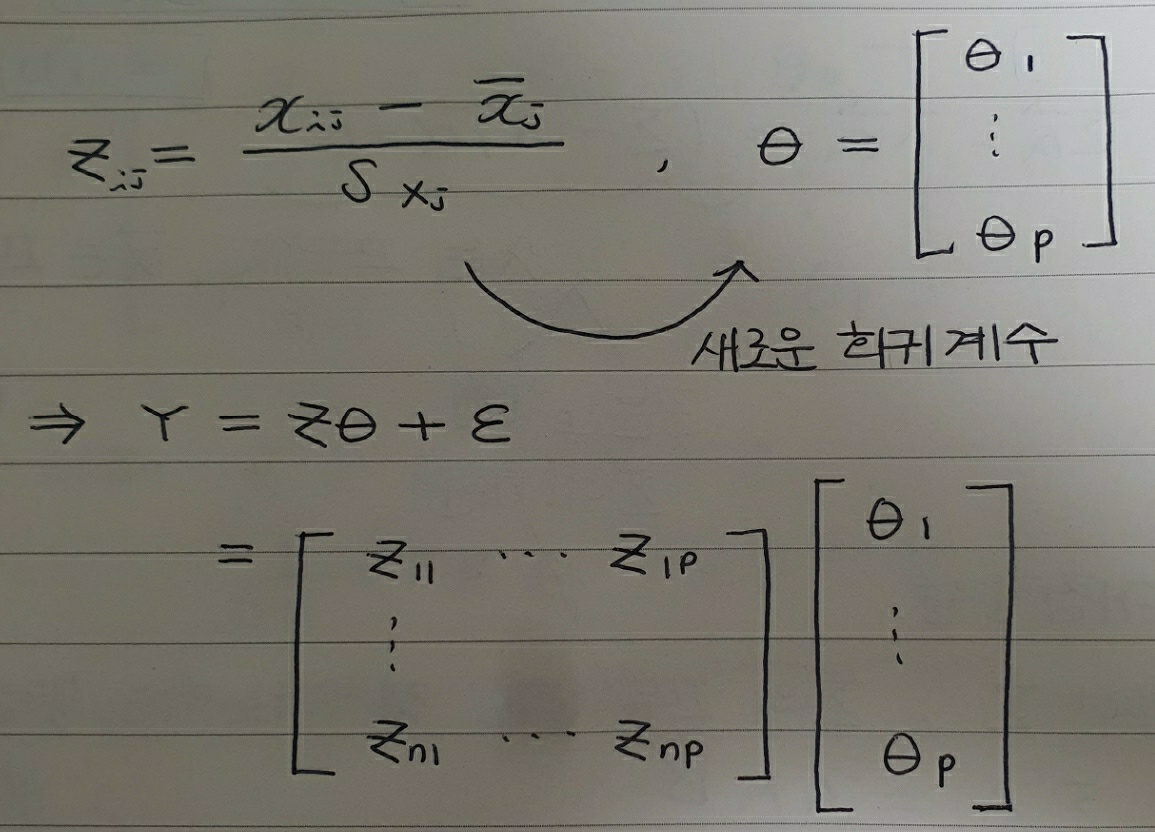
$X$를 표준화한 행렬을 $Z$라고할 때, 우리는 새로운 회귀계수에 대해 상수항이 없는 행렬식을 얻을 수 있습니다.
공분산의 정의를 생각해볼 때 $(Z^TZ)/n-1$는 공분산 행렬이 됩니다. 지금부터는 공분산 행렬 $(Z^TZ)/n-1 = \sum$라고 하겠습니다.
독립변수 행렬은 잠시 두고, PCA에 대해 다시 생각해보도록 하겠습니다. PCA는 기존 변수를 조합해 새로운 변수를 만드는 기법으로, 기존 변수를 선형 결합해 새로운 변수, 주성분을 만들어냅니다.
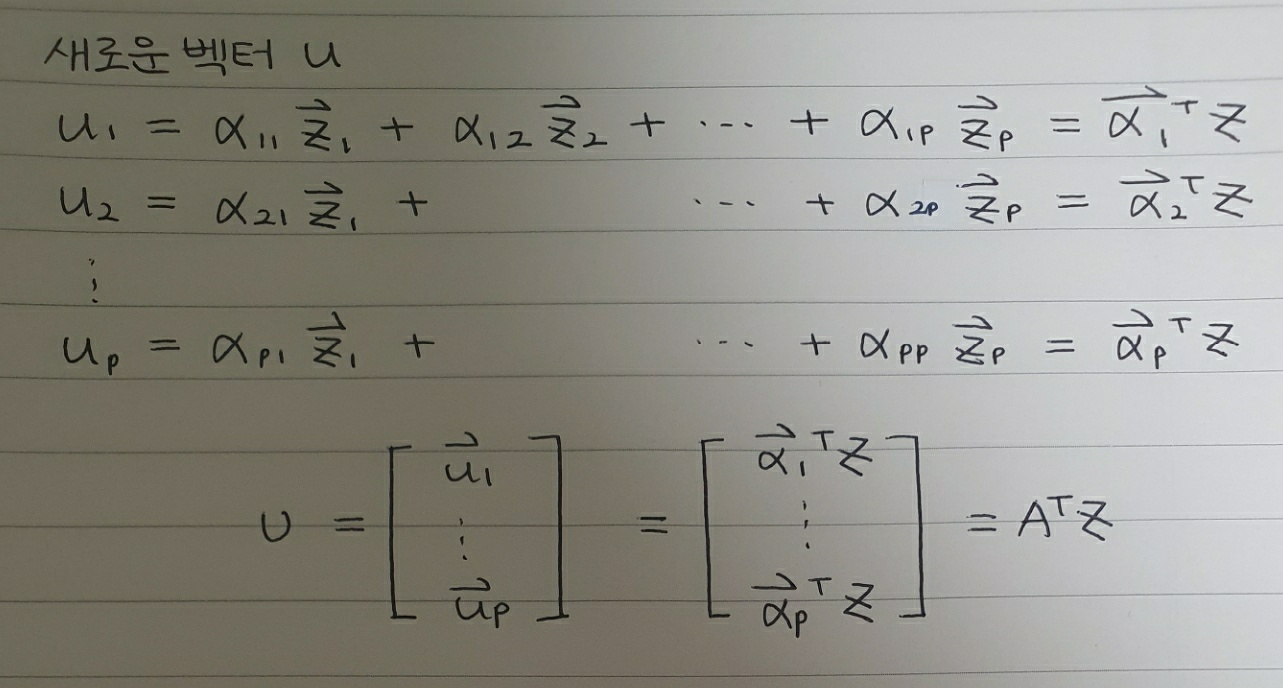
위와 같은 선형 결합은 선형 변환으로도 이해할 수 있습니다. 선형 변환으로 이해하면 벡터 $u_i$는 $X$를 $\alpha$라는 새로운 축에 사영시킨 결과물로 생각할 수 있습니다.
이제 우리는 각 변수와 결합하는 계수 $\alpha$만 알면 PCA를 수행할 수 있습니다. 앞서 설명했듯이 새로운 기저는 원 데이터의 분산을 최대한 보존하고 있기 때문에 $U$의 분산 또한 최대화되어야 합니다.
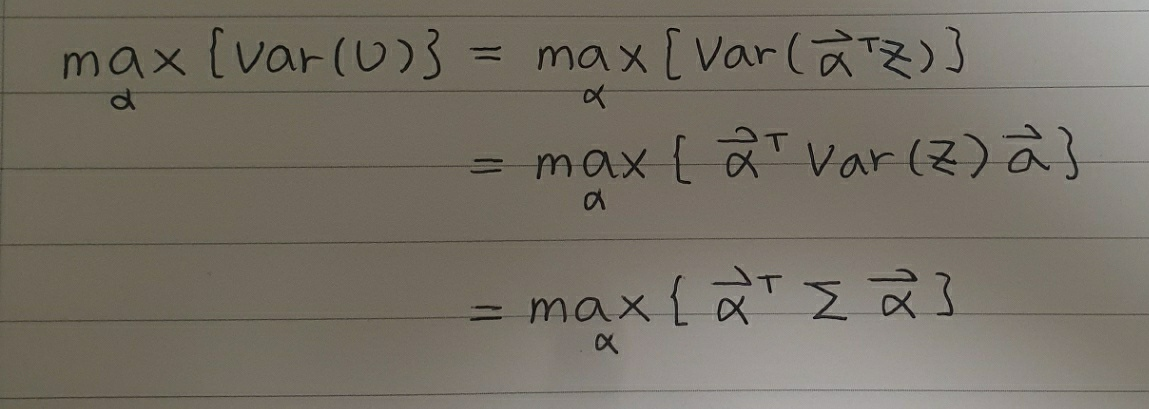
위에서 $X$를 표준화한 행렬 $Z$의 분산을 $\sum$으로 둔 것을 이용해, 행렬 $U$의 분산을 위와 같이 정리할 수 있습니다. 그런데 정리한 마지막 식의 경우 단순히 $\alpha$ 값을 키워 $U$의 분산을 키울 수 있기 때문에, $\alpha$의 크기에 대한 제약식이 필요합니다. 이 제약식(= $alpha$는 단위 벡터)을 종합해 라그랑주 문제로 변형 후, 식을 미분하면 아래와 같습니다.

그런데 가장 아래의 식을 어디서 본 것 같지 않나요? 이 식은 고유 벡터와 고윳값을 정의하는 식($Ax=\lambda x$)과 그 꼴이 같습니다. $\sum$이 행렬, $\lambda$는 스칼라, $\alpha$가 벡터이기 때문에 고유 벡터의 정의와 정확히 일치합니다. 따라서 $\alpha$는 $Z$의 공분산 행렬의 고유 벡터, $\lambda$는 고유값이 됩니다. 따라서 우리는 데이터 $X$를 표준화한 $Z$의 분산을 최대화하는 $\alpha$는 $\sum$의 고유벡터라는 사실을 알 수 있습니다.
이 때 공분산 행렬 $\sum$은 p x p 크기의 정방행렬이자 전치 결과가 자기 자신과 같은 대칭행렬입니다. 열 벡터가 공분산 행렬 $\sum$의 고유 벡터인 행렬을 A, 대각 성분이 $\sum$의 고윳값인 대각행렬을 $\Lambda$라고 할 때 고유 벡터와 고윳값의 정의에 따라 아래와 같이 식을 쓰고 정리할 수 있습니다.
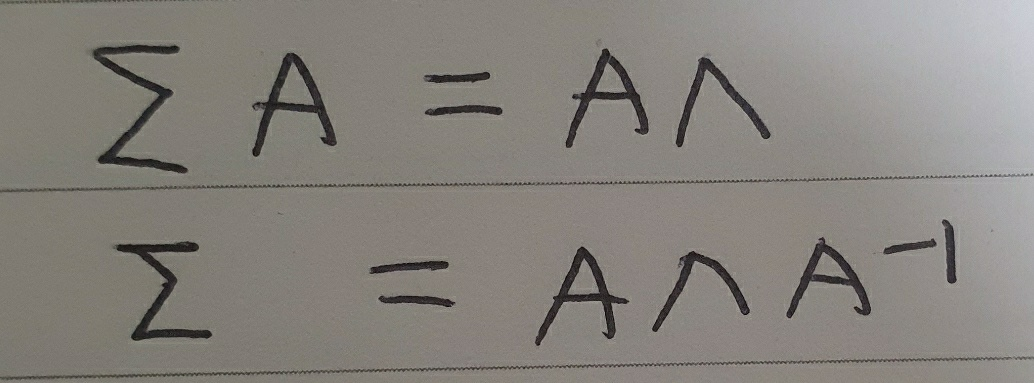
이때 $\sum$이 대칭행렬인 점을 이용하면 아래와 같이 정리할 수 있습니다.
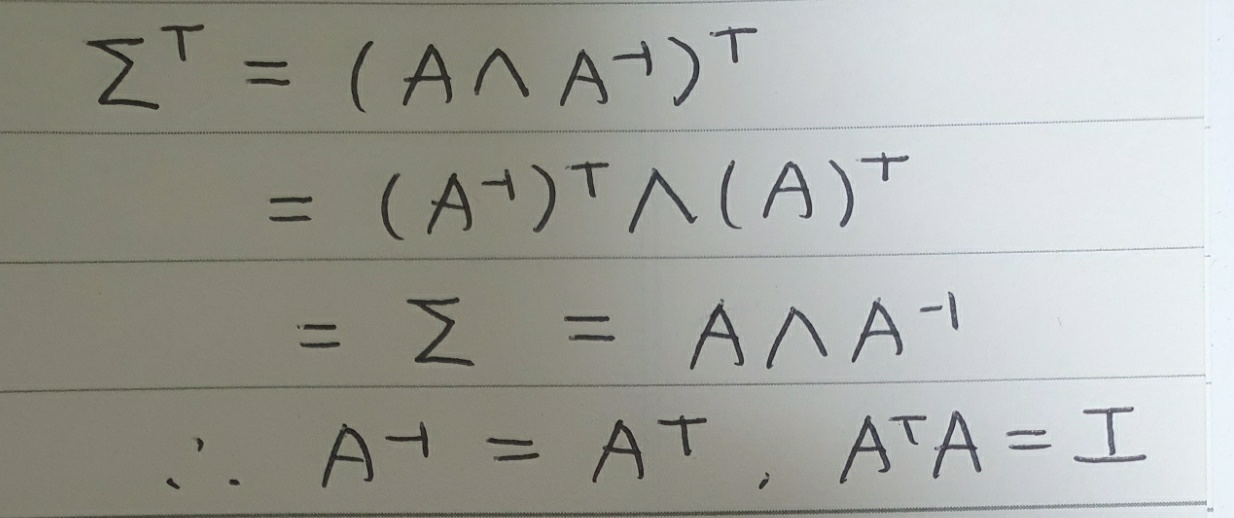
우리는 위의 성질을 이용해 회귀식을 아래와 같이 다시 정리할 수 있습니다.
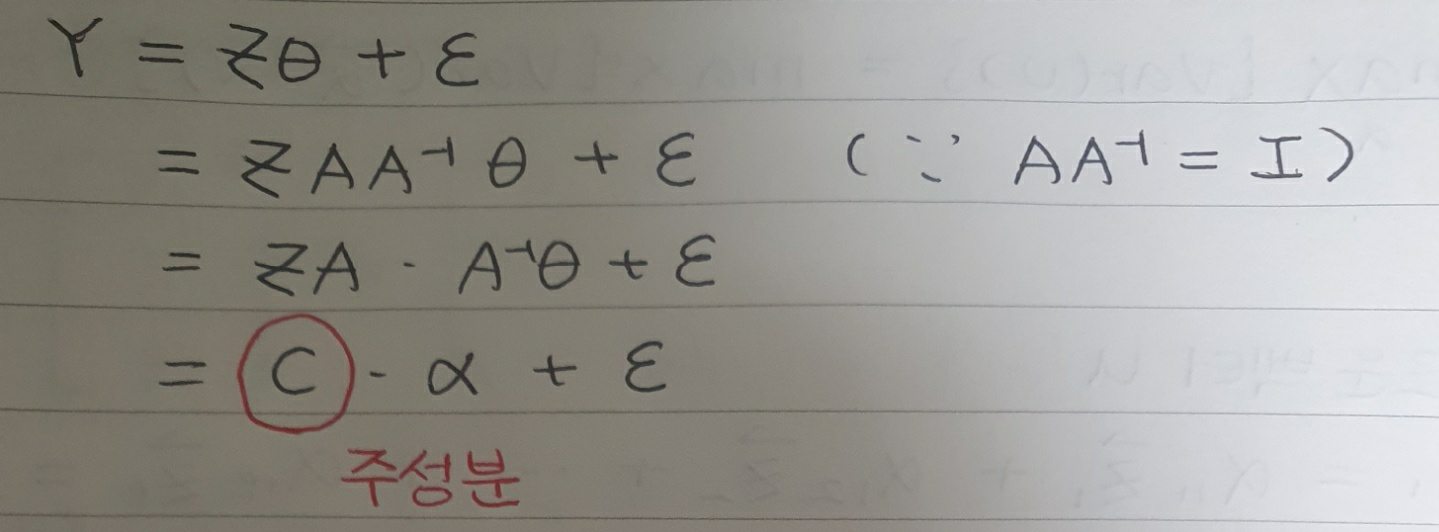
위의 식에는 PCA의 핵심이 모두 나타납니다. 위에서 언급했듯이, PCA는 원 데이터의 분산이 큰 방향을 방향으로 가지는 벡터를 새로운 축, 즉 주성분을 설정하는 것이 그 목적입니다. 그리고 우리는 그 주성분($C$)을 원 데이터의 공분산 행렬($\sum$)의 고유 벡터($\alpha$)를 원 데이터(여기서는 표준화한 데이터 $Z$)와 곱함으로써 구할 수 있습니다.
이때 새로운 변수 $u$의 분산은 무엇일까요? 지금까지 이용한 정의를 이용해 벡터 $u_1$의 분산은 아래와 같이 표현할 수 있습니다.

그리고 고유 벡터의 정의에 의해 위 식을 아래와 같이 정리할 수 있습니다.

이것은 $\sum$의 제1 고유 벡터로 만든 새로운 변수 $u_1$의 분산이 고윳값 $\lambda_1$이라는 것을 의미합니다.
이 고윳값은 회귀분석에서 다중공선성을 진단할 때 사용하기도 합니다. Condition number, 한글로는 상태 지수라고 불리는 이 값은 고윳값 중 가장 큰 값을 가장 작은 값으로 나눈 비율에 루트를 씌워 정의합니다. ($\sqrt {\lambda_1 / \lambda_p}$) 변수 간의 상관관계가 클수록 분산, 즉 $\lambda_p$가 0에 가까워지기 때문에 변수들이 다중공선성을가진다면 상태지수는 큰 값을 갖게 됩니다. 일반적으로 상태지수가 10~15 이상을 나타내면 변수간에 다중공선성이 있다라고 판단하게 됩니다. 그리고 우리는 비정상적인 분산을 갖는 변수들을 제거함으로써 다중공선성 문제를 해결할 수 있습니다. 원래 회귀분석과 비교했을 때 적은 수의 변수를 사용하기 때문에 PCA를 차원 축소 기법이라고 부르기도 합니다.
지금까지 우리는 선형대수를 이용해 PCA에 대해 알아보았습니다. 선형대수에 대한 수리적, 기하적 관점이 모두 동원되어야 이해할 수 있는 부분이기 때문에 다양한 애니메이션, 영상 자료를 참고해 고윳값, 고유 벡터 등에 대한 감을 잡으신 후 다시 PCA를 공부해보실 것을 추천드립니다. 저 역시 선형대수학을 공부했음에도 아무런 관점도 가지지 못해, 선형대수학부터 다시 공부했습니다.😂🤣😅
Reference
https://pathmind.com/kr/wiki/eigenvector
'공부방 > Mathematics' 카테고리의 다른 글
| [선형대수] Ch4. 고유값 분해 (5) | 2021.04.25 |
|---|---|
| [선형대수] Ch3. Least Square (0) | 2021.04.21 |
| [선형대수] Ch2. 선형시스템 및 선형 변환 (0) | 2021.04.19 |
| [수리통계학] Properties of Point estimator and Methods of Estimation - MVUE 계산 흐름 정리 (4) | 2020.12.17 |