www.edwith.org/ai251/joinLectures/195088
인공지능을 위한 선형대수 강좌소개 : edwith
- 주재걸 교수
www.edwith.org
주재걸 교수님의 <인공지능을 위한 선형대수> 강의를 듣고 개인적으로 정리한 글입니다. 공부하면서 지속적으로 업데이트 될 예정입니다. 잘못된 내용에 대한 지적은 댓글로 부탁드립니다. :)
Eigenvectors and Eigenvalues

Eigenspace
- Q. 고유값과 고유벡터는 유일할까?
A. 고유값은 유일하지만, 고유벡터는 무수히 많다. A(cx) = λ(cx)
- 무수히 많은 고유벡터들이 형성하는 부분 공간이 바로 고유공간(eigenspace)
Null Space
- 선형방정식 Ax=b에서 b가 영벡터일 때 식을 만족시키는 모든 가능한 해 x에 대한 집합
- 어떤 Null space든지 반드시 영벡터를 포함함. → '벡터 공간'을 정의할 수 있는 기회가 생김.
+ 벡터 공간

- Null space는 위의 조건들을 만족하기 때문에 Null space는 벡터 공간(부분 공간)이다!
- Q. 그렇다면 b가 영벡터가 아닌 임의의 값을 가질 때에도 해에 대한 벡터 공간이 존재하는가? (해들이 벡터공간을 이루는가?)
A. No! 해 중에 영벡터가 없을 수 있기 때문에 ( = 원점을 지나지 않기 때문에) 0이 아닌 임의의 벡터 b에 대한 해의 벡터 공간은 존재하지 않는다.
- 기하학적인 관점에서...


+ Dim / Rank
① Dim
- 기저 벡터의 개수 (ex. 3차원 공간은 3개의 기저 벡터가 필요하다)
- Q. 행렬 A의 열공간과 행공간의 차원은 같을까?
A. Yes! (직사각행렬이더라도 선형 독립 고려하면...)
② Rank
- 행렬의 열벡터에 의해 span된 벡터공간의 차원
Orthogonal Complement (직교 여집합)
: 벡터 z와 부분공간 W의 모든 벡터가 수직일 때, z가 W에 수직이라고 한다. 이 때, 부분공간 W와 직교인 모든 벡터를 모아 놓은 집합을 W의 직교 여집합(직교 여공간)이라고 부른다. (TMI. Wㅗ 라고 쓰고 W perpendicular 혹은 W perp라고 읽는다)
- Fact
① 어떤 벡터 x가 Wㅗ 안에 존재하기 위한 필요충분조건은 W를 span하는 모든 벡터와 직교라는 것.
② Wㅗ는 Rn의 부분공간이다.
Fundamental Subspaces
- 임의의 행렬 A가 주어졌을 때 4개의 주요 부분 공간이 있다고 한다.
ㄴ Column space / Null space / Row space / Left null space

Gilbert strang 선생님께서 위 그림을 이해하면 선형대수의 절반을 이해한 것과 같다고 하셨다는데😖...

Characteristic Equation (특성 방정식)
- (A-λI)가 역행렬이 존재하는 행렬(= 가역행렬, 정칙 행렬)일 경우 (A-λI)x= 0을 만족하는 영벡터가 아닌 x 벡터는 존재하지 않게 된다. 따라서 (A-λI)의 행렬식을 통해( = 역행렬 존재 판단식) eigenvalue 값을 구할 수 있게 된다.
Diagonalization (대각화) = Eigen decomposition (고유값 분해)

(사실상 같은 식이고, 어떻게 바라보는지에 따라 다르게 부르는 것 같다.)

+ 대부분의 행렬은 n개의 독립인 고유 벡터를 가진다.
고유값 분해와 선형 변환
- 아이디어

- 과정
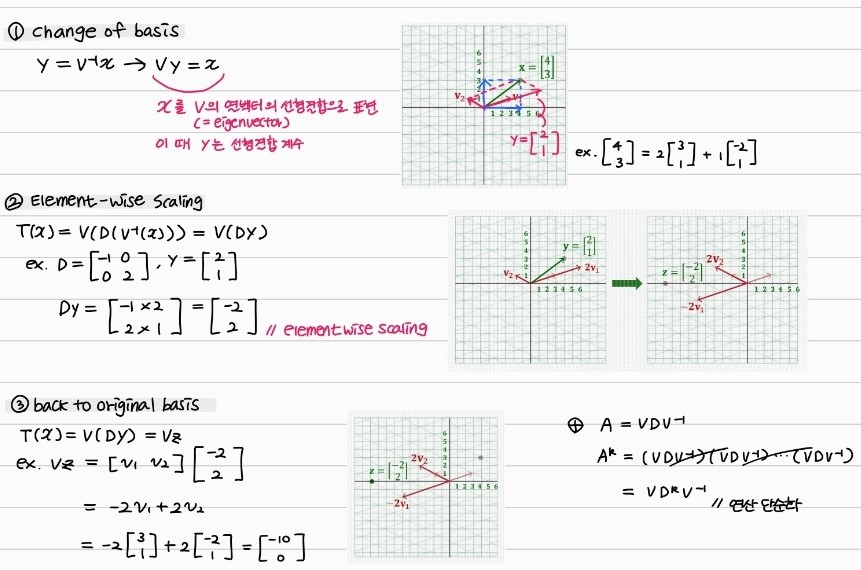
Q. Back to original basis라는 표현을 사용했는데, [-10 0 ] .T 라는 벡터 표현은 [1 0].T, [0 1].T를 basis로 상정한 것이라고 봐야하나? [-10 0 ] .T 은 basis netural(?) 한 표현이라고 생각했는데...
이렇게 눈이 탁 뜨이는 느낌을 주는 공부는 넘모 재밌다 😆
전공기초 수업 들을 때 한 번에 잘 했더라면 좋았을텐데...
'공부방 > Mathematics' 카테고리의 다른 글
| [선형대수] Ch3. Least Square (0) | 2021.04.21 |
|---|---|
| [선형대수] Ch2. 선형시스템 및 선형 변환 (0) | 2021.04.19 |
| [수리통계학] Properties of Point estimator and Methods of Estimation - MVUE 계산 흐름 정리 (4) | 2020.12.17 |
| 선형대수로 알아보는 PCA(주성분 분석) (0) | 2020.06.13 |