[4] Risk Adjusted Returns (RAR) / Diversification and Portfolio Optimization / Portfolio Analysis

Risk Adjusted Returns (RAR)

- 어떤 펀드 혹은 포트폴리오가 더 나은지 비교, 결정할 수 있는지?
- RAR metric 통해 Risk와 Return 모두 고려

 

Sharpe ratio

- 일반적으로 사용되는 RAR measure
- the average return earned in excess of the risk-free rate per unit of volatility or total risk

- risk-free rate : 무위험 수익률. 말 그대로 위험이 전혀 없는 보장된, 이론적인 수익. 투자에서 위험이 전혀 내포되지 않은 순수한 투자의 기대수익률.

 

- 실제 계산은 다음과 같이 한다.

- 분자) Adj Close의 percent change의 평균 - (risk_free_ann_ret_rate / 252)
- 분모) 포트폴리오의 excess return
             = (Adj Close의 percent change 시리즈 - (risk_free_ann_ret_rate/252) )의 std

- sharpe = 분자/분모 * root(252)

 

Risk Adjusted Return

- 이 값이 0보다 작다는 것은 risk-free alternative보다 성과를 거두지 못한다는 뜻 

 

Calculating Sharpe Ratio from Daily Prices

- Sharpe ratio는 daily RAR. root(252)를 곱해 annualized RAR 계산

 

Alternative RAR Measure

- Upside volatility에는 페널티를 주지 않는 Sortino ratio도 있음

 

---

Diversification and Portfolio Optimization

- 어떻게하면 적은 risk로 유사한 return을 얻을 수 있을까?
- 즉, RAR을 어떻게 향상/최적화 할 수 있을까?

- 일반적으로 Annualized return과 함께 volatility는 증가함. (High returns, High risk) 하지만 꼭 Tradeoff가 있어야할까?

 

- 만약 Foo와 InvFoo에 예산 절반씩을 배정한다면 결과는 어떨까?

- 하지만 현실에는 완벽하게 inversely correlated하면서 같은 return을 갖는 instrument는 없음. 하지만 inversely, non correlated instruments는 있음.

- 이 경우, RAR이 foo보다는 좋지만 Bar보다 좋을 수는 없음. Bar의 volatility가 매우 낮기 때문에. (의도적인 설정) 이렇게 낮은 volatility를 갖고 있을 경우 RAR을 향상시키기 어려움.

 

Portfolio Optimization

- 다른 상관관계를 갖는 instruments를 섞어, 포트폴리오 전체의 volatility를 낮출 수 있음
- 이 경우 전체 return은 낮아지지만, RAR을 향상시킬 수 있음
- low or negative correlation의 포트폴리오 조합을 만드는 것이 중요함

 

eg. 50% SPY + 50% TLT

 

---

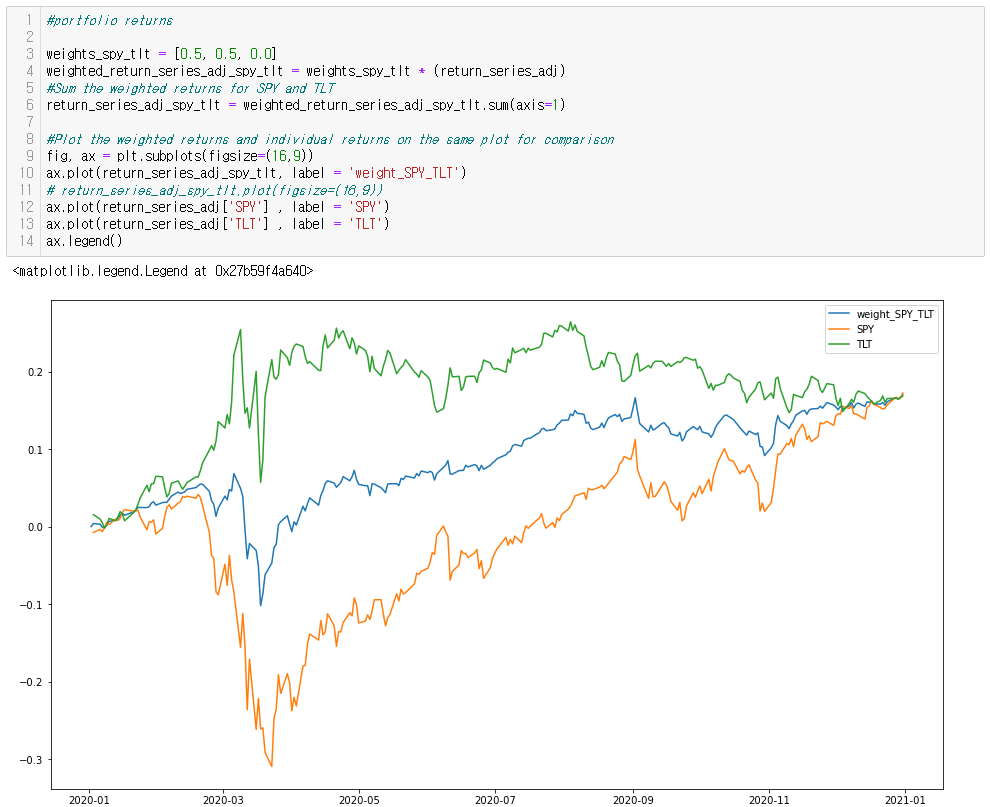
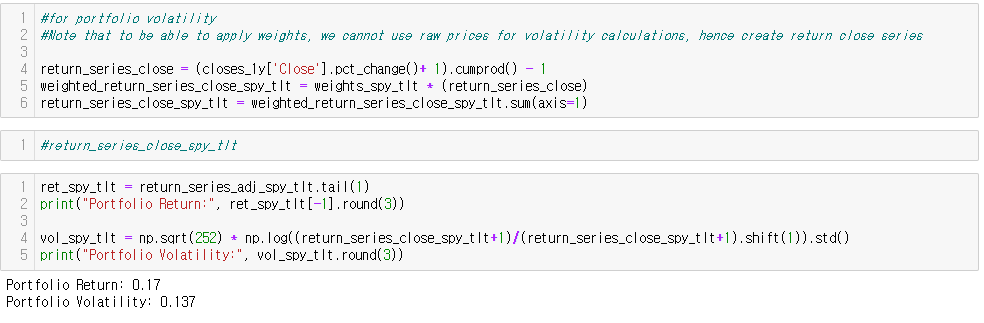
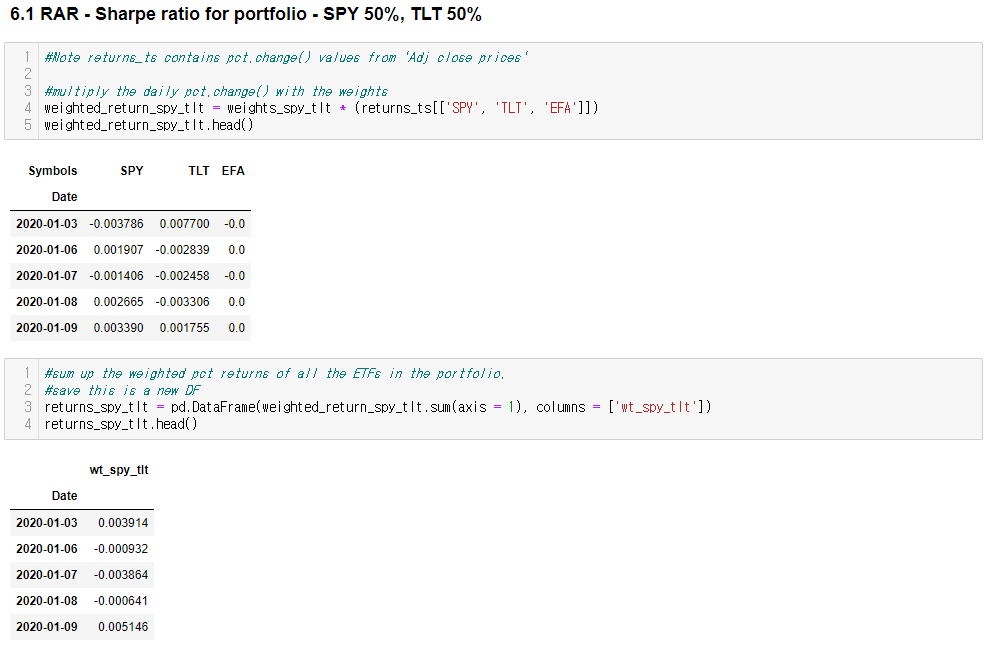
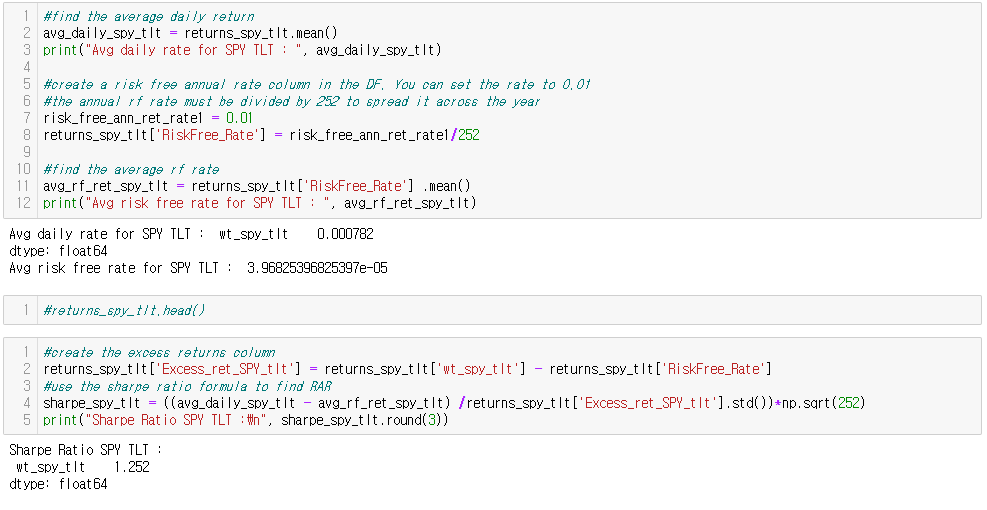
Portfolio Analysis

- pyfolio 패키지를 이용해 portfolio statistics 계산 (Annual return, Annualized volatility, Sharpe ratio 등 계산 가능)

- pf.create_simple_tear_sheet(portfolio_returns)
ㄴ 이때 portfolio_returns는 daily percent change

 

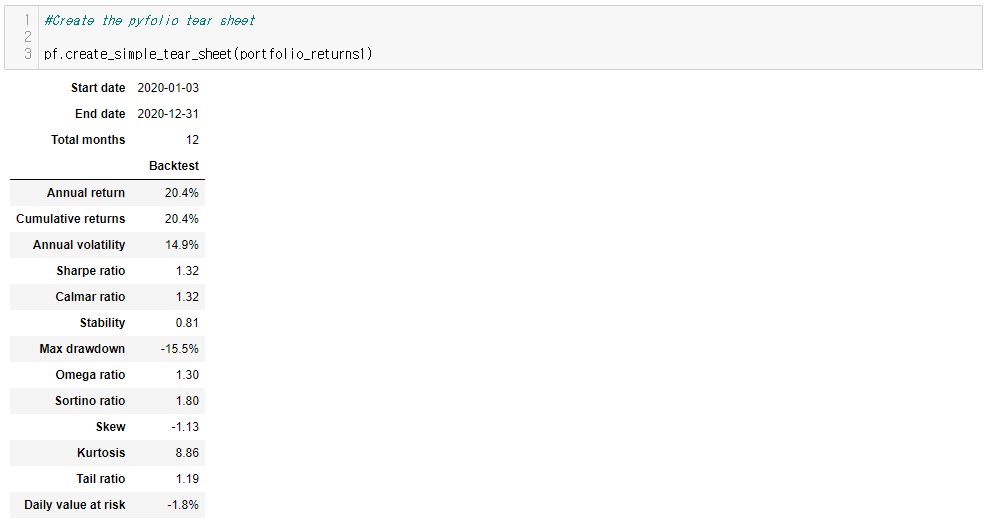
Tear sheet

- 금융계에서 tear sheet는 각각의 회사 또는 펀드에 대한 주요 정보를 요약한 서류를 의미함